La operación básica al aplicar el criterio de Nyquist es un Mapeo del plano S al plano F(s). Este documento presenta el criterio de estabilidad de Nyquist y sus fundamentos matemáticos. Sea el sistema de lazo cerrado que se ve en la Fig. No. 1. La función transferencia de lazo cerrado es :
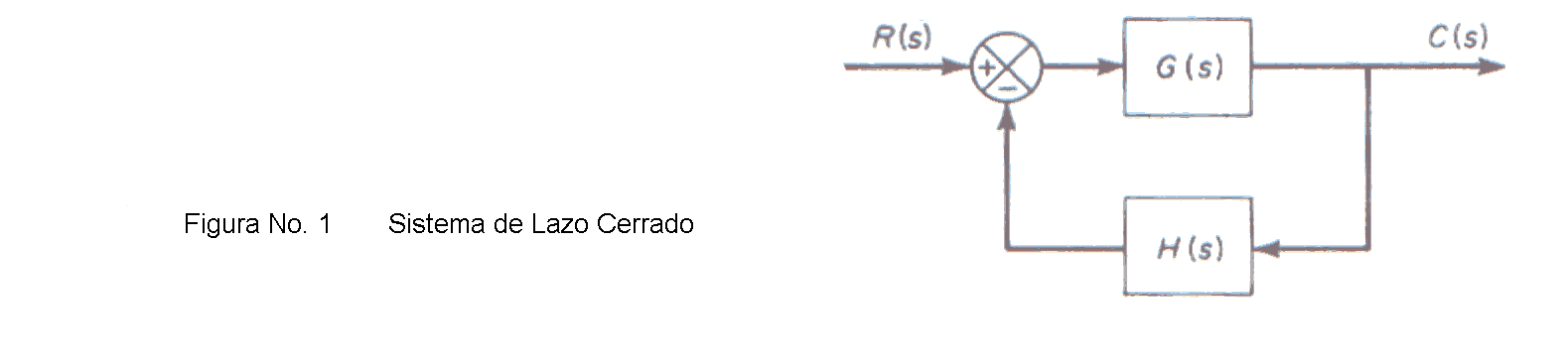
Se tendrá estabilidad cuando todas las raíces de la ecuación característica
1 + G(S)H(S) = 0
estén en el semiplano izquierdo s. El criterio de estabilidad de Nyquist relaciona la respuesta de frecuencia de lazo abierto G(jω) H(jω) a la cantidad de ceros y polos de 1 + G(s) H(s) que hay en el semiplano derecho s. Este criterio debido a H. Nyquist es ϊtil en ingeniería de control porque se puede determinar gráficamente de las curvas de respuesta de lazo abierto la estabilidad absoluta del sistema de lazo cerrado, sin necesidad de determinar los polos de lazo cerrado. Se pueden utilizar para el análisis de estabilidad las curvas de respuesta de frecuencia de lazo abierto obtenida analíticamente o experimentalmente. Esto es muy conveniente porque al diseñar un sistema de control frecuentemente sucede que para algunos componentes no se conoce la expresión matemática y solo se dispone de datos de su característica de respuesta de frecuencia.El criterio de estabilidad de Nyquist esta basado en un teorema de la teoría de las variables complejas. Para entender el criterio primero se han de tratar los con tornos de transformación en el plano complejo.
Se supone que la función transferencia de lazo abierto G(s) H(s) es representable como una relación de polinomios en s. Para un sistema físicamente realizable, el grado del polinomio denominador de la función transferencia de lazo cerrado, debe ser mayor o igual al del polinomio numerador. Esto significa que el limite de G(s) H(s) es cero o una constante para cualquier sistema físicamente construible, al tender s hacia infinito.
Estudio preliminar.
La ecuación característica del sistema que se ve en la Fig. No.1 es
F(s) = 1 + G(s)H(s) = 0
Se ha de demostrar que a un camino cerrado continuo dado en el plano s que no pasa por ningún punto singular, corresponde una curva cerrada en el plano F(s).La cantidad y sentido de lazos o rodeos alrededor del origen en el plano F(s) por una curva cerrada, juega un papel importante en lo que sigue, pues mas adelante se ha de relacionar la cantidad y sentido de lazos o rodeos con la estabilidad del sistema.
Sea, por ejemplo, la siguiente función transferencia de lazo abierto:
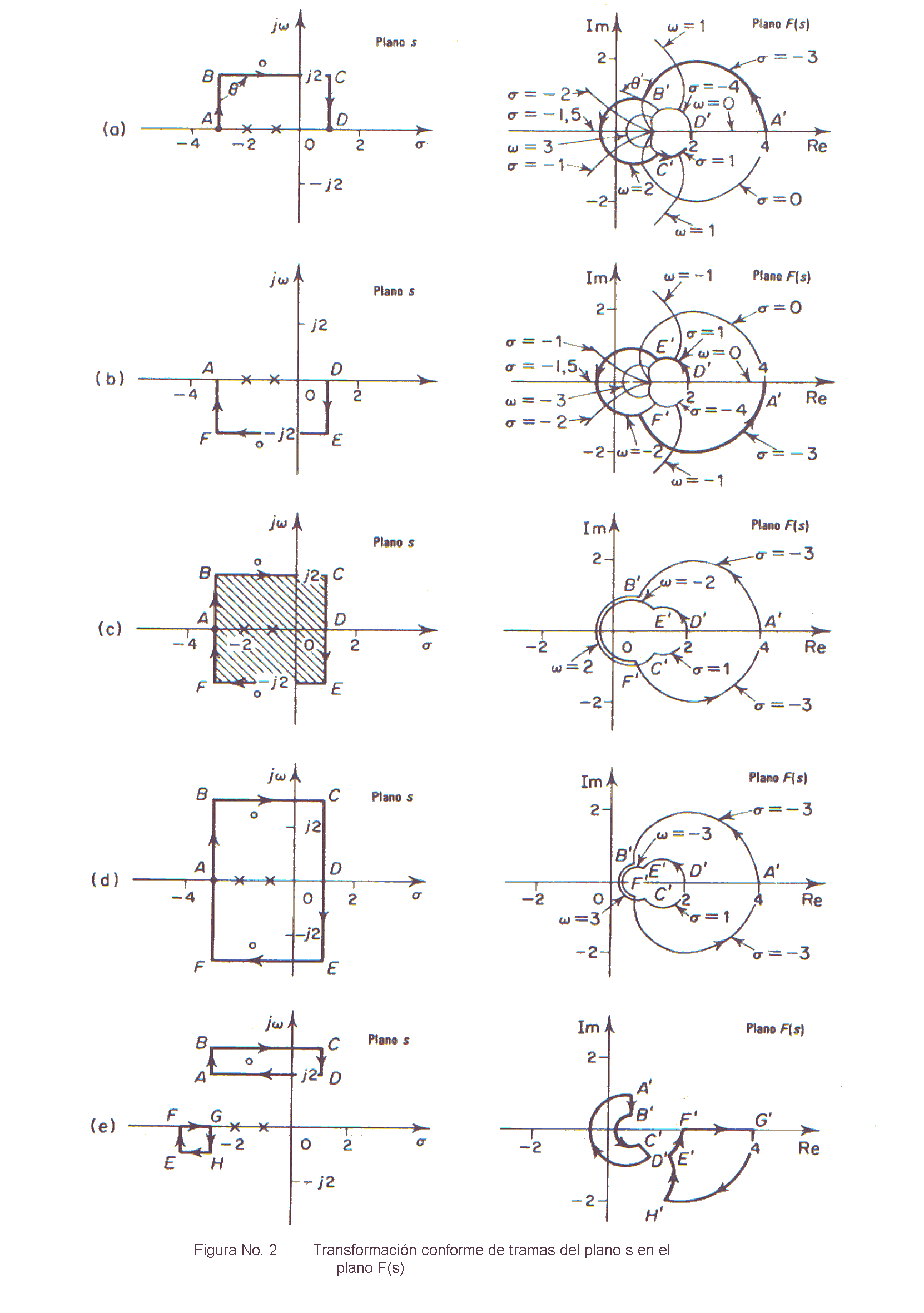
Entonces, como se indicó antes, para un trayecto cerrado continuo dado en el plano s, que no atraviesa ningún punto singular, corresponde una curva cerrada en el plano F(s). La Fig. 2 (a) muestra representaciones conformes de las líneas ω = 0, 1, 2, 3 y de las líneas σ = 1, 0, - 1, - 2, - 3, - 4 en el semiplano superior s, al plano F(s). Por ejemplo, la lνnea s = jω en el semiplano superior s(ω ≥ 0) se transforma en la curva indicada por σ = 0 en el plano F(s). La Fig. 2 (b) muestra representaciones conformes de las lνneas ω = 0, - 1, - 2, - 3 y las lνneas ω = 1, 0, - 1, - 2, - 3, - 4 en el semiplano inferior s al plano F(s). Se hace notar que para un valor dado de σ la curva para frecuencias negativas es simιtrica respecto al eje real con la curva para frecuencias positivas con referencia a las Figuras 2 (a) y (b) se ve que para el trayecto ABCD en el plano s recorrido en el sentido horario, la curva correspondiente en el plano F(s) es A'B'C'D'. Las flechas en las curvas indican los sentidos de recorrido. En forma similar, el recorrido DEFA en el plano s, se transforma en la curva D'E'F'A' en el plano F(s). Debido a la propiedad de la transformación conforme, los ángulos correspondientes en el plano s y en el plano F(s) son iguales y tienen el mismo sentido. (Por ejemplo, como las líneas, AB y BC se cortan entre si en ángulos rectos en el plano, también se cortan en ángulos rectos en el punta B' las curvas A'B'y B'C' en el plano F(s.)) Con referencia. a la Fig. 2 (c), se ve que en el contorno cerrado ABCDEFA en el plano s, la variable s comienza en el punto A y toma a lo largo de su camino valores en sentido horario hasta retornar al punto de partida A. La curva correspondiente en el plano F(s) queda indicada por A'B'C'D'E'F'A'. Si se define el Área a 1a derecha del contorno cuando el punto representativo s, se desplaza en la dirección horaria, como contenido en el contorno y al Área a la izquierda como exterior a ese entorno, el Área sombreada en la Fig. 2 ( c) esta encerrada. por el contorno ABCDEFA y esta dentro de él. De la Fig. 2 ( c ) se puede ver que cuando el contorno en el plano s, incluye dos polos de F(s), el lugar de F(S) incluye el origen del plano F(s) dos veces en la dirección antihorario.
La cantidad de rodeos al origen en el plano F(s) depende del contorno cerrado en el plano s. Si ese entorno incluye dos ceros y dos polos de F(s), el lugar correspondiente F(s) no incluye el origen, como puede verse en la Fig 2 (d). Si este contorno contiene solamente un cero, el lugar correspondiente de F(s) engloba el origen una vez en la dirección horaria. Puede verse esto en la Fig. 2 (e). Finalmente, si el contorno cerrado en el plano s no incluye ni ceros ni polos, entonces el lugar de F(s) no incluye el origen del plano F(s). También se puede ver esto en la Fig. 2 (e).
Se hace notar que para cada punto en el plano s, excepto para los puntos sin- gulares, hay sólo un punto correspondiente en el plano F(s); es decir, que la trans- formación del plano s en el plano F(s) es uno-a-uno. Sin embargo, la transformación del plano F(s) en el plano s, puede no ser univoca, de manera que para un punto dado en el plano F(s), puede corresponder mas de un punto en el plano s. Por ejemplo, el punto B' en el plano F(s) en la Fig. 2 (b), corresponde tanto al punto (- 3, 3) como al punto (0, - 3) en el plano s.
Del análisis precedente, se puede ver que el sentido en el que se rodea el origen en el plano F(s) depende de si el contorno en el plano s incluye un polo o un cero. Se hace notar que la ubicación de un polo o cero en el plano s, sea en la mitad derecha o izquierda del plano s, no produce ninguna diferencia, pero si la produce el rodeo de un polo o un cero. Si el contorno del plano s incluye k ceros y k polos (k = 0, 1, 2, ...), es decir igual cantidad de cada uno, la correspondiente curva cerrada en el plano F(s) no encierra el origen del plano F(s). La discusión precedente es una explicación gráfica del teorema de representación, que es la base del criterio de estabilidad de Nyquist.
Teorema de la representación
Sea F(s) la relación entre dos polinomios en s. Sea P el número de polos y Z el número de ceros de F(s) que quedan dentro de un contorno determinado del plano s, considerando inclusive la multiplicidad de polos y ceros. Sea este contorno tal que no pasa por ningún polo ni cero de F(s). Este contorno cerrado en el plano s se transforma en una curva cerrada en el plano F(s). A medida que un punto representativo recorre el contorno completo en el plano s en sentido horario, se producen un total de N rodeos en torno del origen en el plano F(s), y ese numero N es igual a Z - P. (Nótese que con este teorema de la representación no se puede hallar la cantidad de polos y ceros, sino su diferencia.)
Un número N positivo indica un exceso de ceros respecto a los polos en la función F(s), mientras N negativo muestra mayor cantidad de polos que de ceros. En aplicación de sistemas de control, se determine fácilmente P para F(s) = 1 + G(s)H(s) de la función G(s)H(s). Por tanto, si se halla N del diagrama de F(s), se determina fácilmente la cantidad de ceros en el contorno cerrado en el plano s. Se remarca que no tienen importancia ni la forma exacta del contorno en el plano s ni el lugar de F(s) en lo que respecta a giros por el origen, ya que los mismos sólo dependen de los polos y/o ceros de F(s) contenidos en el contorno del plano s.
Aplicación del teorema de la representación al análisis de estabilidad de sistemas de lazo cerrado
Para analizar la estabilidad de sistemas de control lineal, se hace que el contorno cerrado del plano s abarque todo el semiplano derecho s. El contorno consiste en todo el eje ω desde (ω = - ∞ hasta ω = +∞) , y un paso semicircular de radio infinito en el semiplano s derecho. Este contorno recibe el nombre de recorrido de Nyquist. (El sentido del mismo es horario.) El recorrido de Nyquist abarca todo el semiplano derecho de s y contiene todos los ceros y polos de 1 + G(s)H(s) con partes reales positivas. (Si no hay ceros de 1 + G(s)H(s) en el semiplano derecho de s, no hay polos de lazo cerrado alli y el sistema es estable.) Es necesario que el contorno cerrado o recorrido de Nyquist no pase por ningún polo o cero de 1 + G(s)H(s). Si G(s) tiene un polo o polos en el origen del plano s, se hace indeterminada la representación del punto s = 0. En esos casos se evita el origen efectuando un desvio alrededor de él. (Más adelante se efectúa una discusión detallada sobre este caso especial.) Si se aplica el teorema de la representación al caso especial en que F(s) es igual a 1 + G(s)H(s) se puede afirmar lo siguiente: si el contorno cerrado en el plano s contiene todo el semiplano s derecho, como se muestra en la Fig. 3, la cantidad de ceros en el semiplano derecho de la función F(s) = 1 + G(s)H(s) es igual a la cantidad de polos de la función F(s) = 1 + G(s)H(s) en el semiplano derecho de s mas la cantidad de rodeos completos horarios al origen del plano 1 + G(s)H(s) de la curva cerrada correspondiente en este último plano. Debido a la condición supuesta de que
lim [1 + G(s)H(s)] =
la función 1 + G(s)H(s) permanece constante mientras s recorre el semicírculo de radio infinito. Debido a esto, se puede determinar si el lugar de 1 + G(s)H(s) Fig. 3.
Contiene o no el origen del plano 1 + G(s)H(s) analizando tan sólo una parte del contorno cerrado del plano s, el eje ωj. Si hay rodeos al origen, se producen únicamente cuando el punto representativo pasa de –j∞ a +j∞ a lo largo del eje ωj, siempre que no haya ceros ni polos sobre el eje ωj.
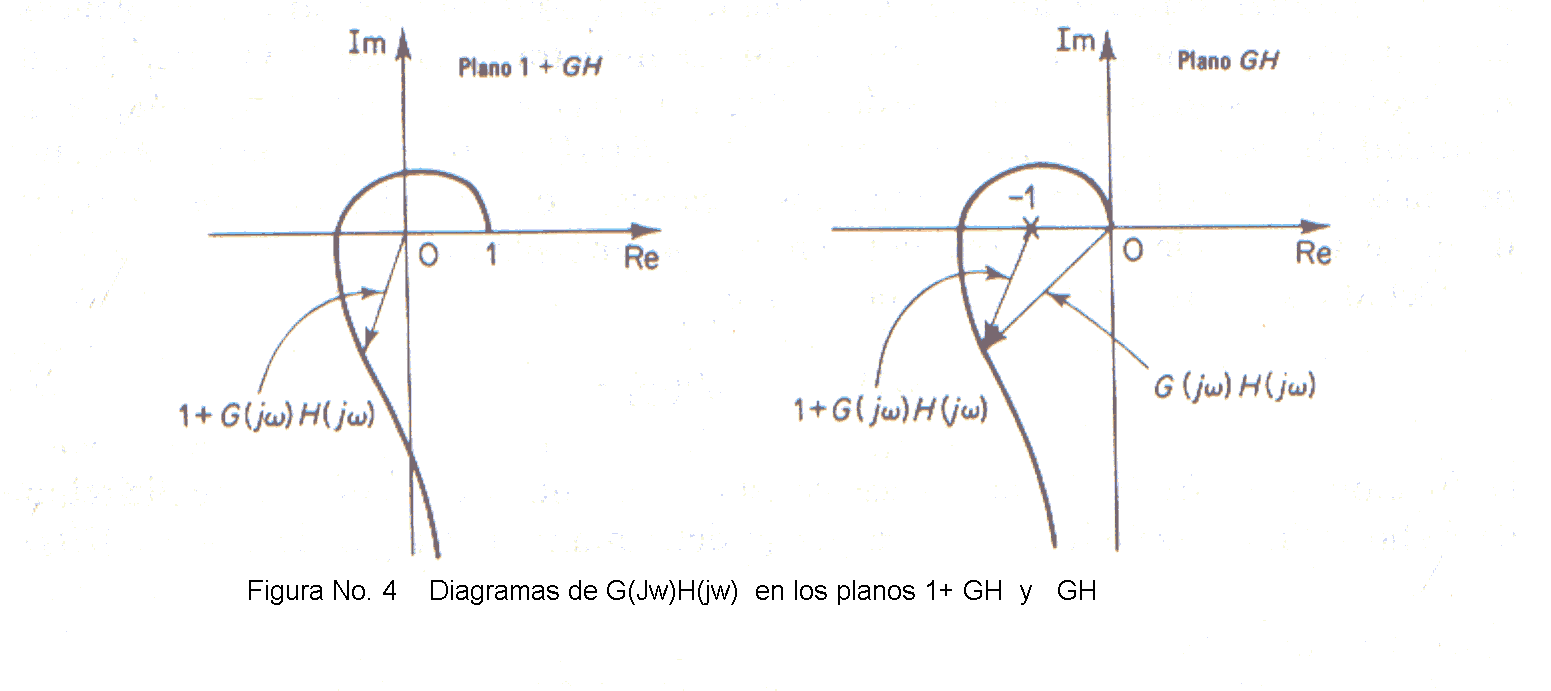
Nótese que la porción del contorno de 1 + G(s)H(s) desde (ω = - ∞ hasta ω = +∞), es simplemente 1 + G(ωj)H(ωj). Como 1 + G(ωj)H(ωj) es el vector suma del vector unitario y el vector G(ωj)H(ωj), el tιrmino 1 + G(ωj)H(ωj) es igual al vector que va desde el punto - 1 + 0j hasta el extremo del vector G(ωj)H(ωj), como se ve en la Fig. 4. Circunscribir el origen por el grafico 1 + G(ωj)H(ωj) equivale a hacerlo con el punto -1 +0j por el lugar de G(ωj)H(ωj). Entonces se puede estudiar la estabilidad de un sistema de lazo cerrado analizando los rodeos del punto - 1 + 0j por el lugar de G(ωj))H(ωj). Se puede determinar la cantidad de giros que incluyen el punto - 1 + 0j trazando un vector desde el punto - 1 + 0j hasta el lugar de G(ωj)H(ωj), comenzando en (ω = - ∞, pasando por (ω = 0, y llegando hasta ω = + ∞ mientras se cuenta la cantidad de rotaciones horarias del vector.
El trazado de G(jω)H(jω) para el recorrido de Nyquist es inmediato. La representación del eje negativo jω es la imagen simétrica del eje positivo jω respecto al eje real. Es decir, el diagrama de G(jω)H(jω) y el de G(jω)H(-jω) son simιtricos respecto al eje real. El semicírculo de radio infinito se transforma en el origen del plano GH o en un punto sobre el eje real del plano GH.
En la exposición precedente, se supuso que G(s)H(s) es la relación entre dos polinomios en s. De modo que ha quedado fuera del análisis el retardo de transporte e-T*s.
Criterio de estabilidad de Nyquist
Se puede resumir el siguiente criterio de estabilidad de Nyquist, basado en el análisis previo, analizando los rodeos del punto - 1 + j0 por el lugar de G(jω)H(jω): Criterio de estabilidad de Nyquist [para un caso especial en que G(s)H(s) no tiene ni polos ni ceros sobre el eje jω]: en el sistema que se presenta en la Fig. 1, si la funciσn transferencia de lazo abierto G(s)H(s) tiene k polos en el semiplano s positivo y
Observaciones sobre el criterio de estabilidad de Nyquist
1. Se puede expresar este criterio como
Z = N + P
DondeZ = cantidad de ceros de 1 + G(s)H(s) en el semiplano derecho de s
N = cantidad de circunscripciones del punto - 1 + j0 en sentido horario
P = cantidad de polos de G(s)H(s), en el semiplano derecho de s
Si P no es cero, para un sistema de control estable se debe tener Z=0, o N=-P lo que significa que hay que tener P rodeos antihorarios del punto - 1 + j0.
Si G(s)H(s) no tiene polos en el semiplano derecho de s, Z = N.

Por tanto, para que haya estabilidad, no debe haber rodeos del punto - 1 + j0 por el lugar de G(s)H(s). En este caso no es necesario considerar el lugar en todo el eje jω, pues basta la porción de frecuencia positiva. Se puede determinar la estabilidad del sistema viendo si el punto - 1 + j0 esta rodeado por el diagrama de Nyquist de G(jω)H(jω). En la Fig. 5, se ve la regiσn incluida en el diagrama de Nyquist. Para tener estabilidad, el punto - 1 + j0 debe quedar fuera de la zona sombreada.
2. Hay que ser muy cuidadoso al verificar la estabilidad de sistemas de lazo múltiple pues pueden incluir polos en el semiplano s derecho. (Se hace notar que si bien un lazo interior puede ser inestable, se puede hacer estable todo el sistema de lazo cerrado con un diseño adecuado.) No basta con la simple inspección de los rodeos del punto - 1 + j0 por el lugar de G(jω)H(jω), para detectar inestabilidad en sistemas de lazo mϊltiple. Sin embargo, en esos casos se puede determinar fácilmente si hay o no algún polo en el semiplano derecho de s, aplicando el criterio de estabilidad de Routh al denominador de G(s)H(s).
Si hay incluidas funciones trascendentes, como retardo de transporte e-Ts en G(s)H(s), se las puede aproximar por una expansión en serie antes de aplicar el criterio de estabilidad de Routh. Una forma de expansión en serie de e-Ts puede ser :
e-Ts = 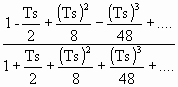
Como primera aproximación, se toman en numerador y denominador, solamente los dos primeros términos, o sea,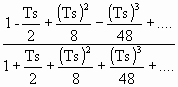
e-Ts = 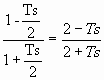
Esto da una buena aproximación al retardo de transporte para el rango de frecuencias 0<ω<(0,5/T). [Se hace notar que el valor de (2 - jωT)/(2 + jωT) es siempre la unidad y que el retardo de fase de (2 - jωT)/(2 + jωT) se aproxima mucho al retardo de transporte dentro del rango de frecuencias indicado.]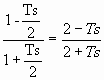
3. Si el lugar de G(jω)H(jω) pasa por el punto - 1 + j0, hay ceros de la ecuación característica o polos de lazo cerrado sobre el eje jω. Esto no es deseable en sistemas de control en la práctica. En un sistema de lazo cerrado bien diseñado ninguna de las raíces de la ecuación característica debe estar sobre el eje jω.
Caso especial en que G(s) H(s) involucra polos y/o ceros sobre el eje jω
En el análisis previo se supuso que la función transferencia de lazo abierto G(s) H(s) no tiene ni polos ni ceros en el origen. Ahora se ha de considerar el caso en que G(s) H(s) tiene polos y/o ceros sobre el eje jω.
Como el recorrido de Nyquist no debe pasar por polos o ceros de G(s) H(s), si la función G(s) H(s) tiene polos o ceros en el origen (o en puntos del eje, jω distintos al origen), hay que modificar el contorno en el plano s. El modo habitual de hacerlo, es modificar el contorno en la vecindad del origen utilizando un semicírculo de radio infinitesimal є, como se ve en la Fig.у. Se mueve un punto representativo s a lo largo del eje jω negativo desde –j∞ hasta j0-. Desde s = j0- hasta s = j0+, el punto se desplaza sobre el semicírculo de radio є (donde є << 1) y finalmente se desplaza a lo largo del eje jω positivo desde j0+, hasta j∞.
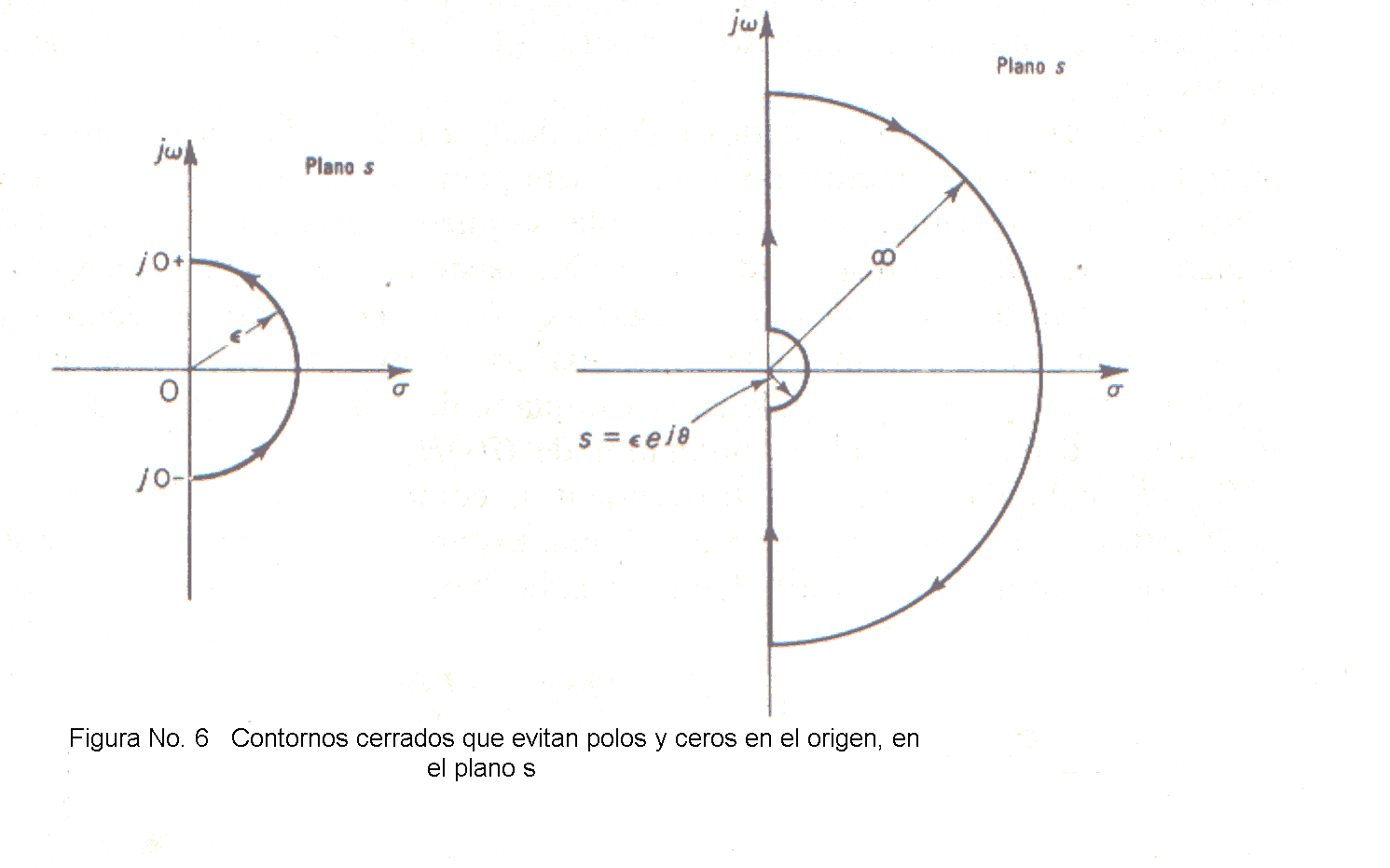
G(S) H(s) = 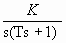
Los puntos correspondientes a s = j0+, y s = j0- en el lugar de G(s)H(s) tienen en el plano G(s)H(s), -j∞ y j∞, respectivamente. En la porción semicircular de radio є (donde є << 1), se puede escribir la variable compleja sS = єejθ
Donde θ varνa de - 90' a +90. Entonces G(s)H(s) es :G(єejθ)H(єejθ) = K/(єejθ) = 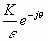
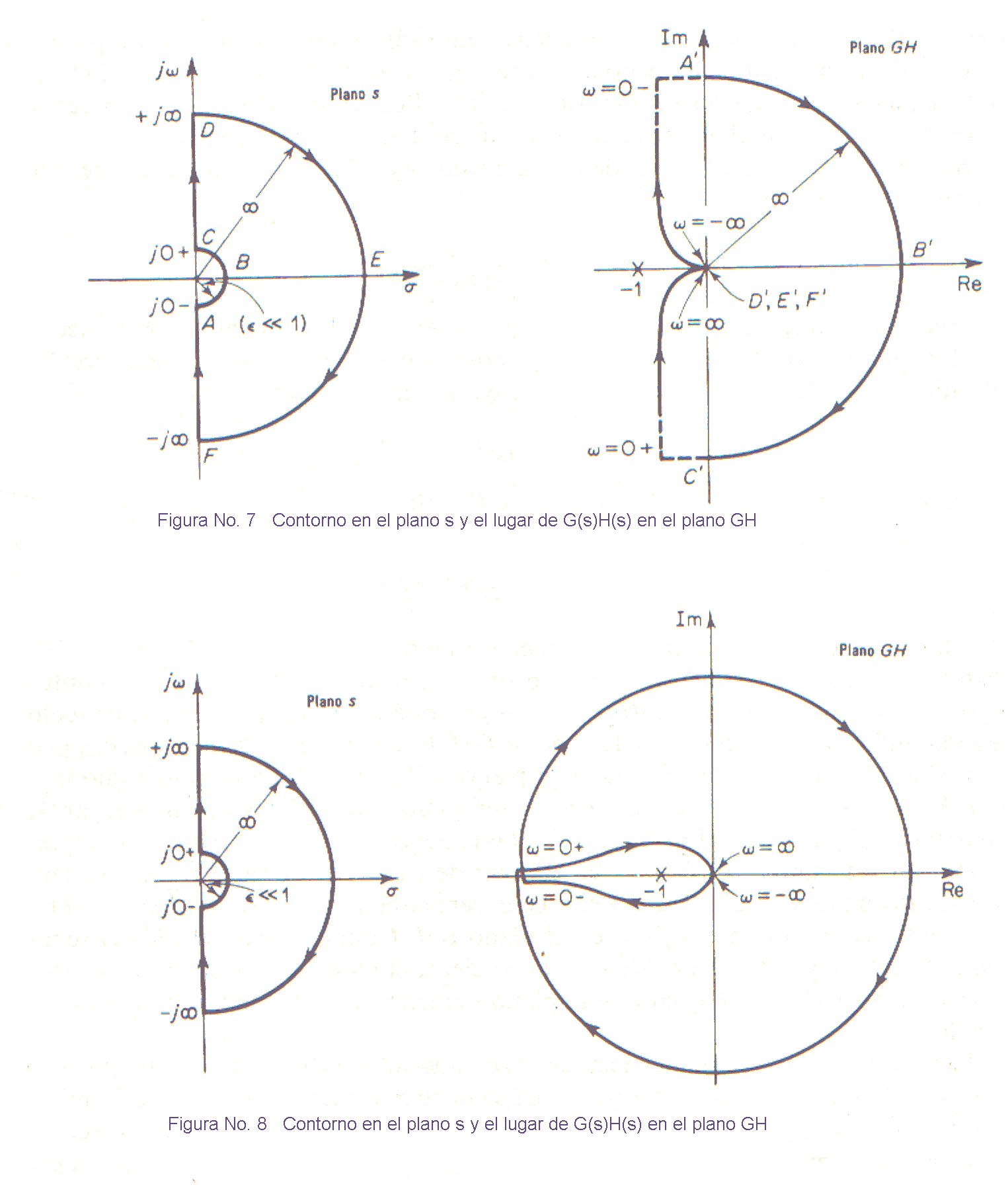
El valor de K/є tiende a infinito al tender є a cero, y -θ varia desde 90' a - 90' cuando el punto representativo s recorre el semicírculo. Entonces los puntos G (j0-) H (j0-) = j∞ y G(j0+)H(j0+) = -j∞ están unidos por un semicírculo de radio infinito en el semiplano derecho de GH. El desvió semicircular infinitesimal alrededor del origen se transforma en el plano GH en un semicírculo de radio infinito. En la Fig. 7 se ve un contorno en el plano s transformado en el lugar de G(s)H(s) en el plano GH. Los puntos A, B y C del contorno en el plano s, se representan por los puntos A' B' y C en el lugar de G(s)H(s). Como se ve en la Figura 7, los puntos D, E y F que están en el semicírculo de radio infinito en el plano s, se transforman en el origen en el plano GH. Como no hay polo en el semiplano derecho s y el lugar de G(s)H(s) no encierra el punto - 1 + j0, no hay ceros de la función 1 + G(s)H(s) en el semiplano derecho de s. Por tanto, el sistema es estable.Para una función transferencia de lazo abierto G(s)H(s) con un factor 1/sn (con n = 2, 3 .... ), el diagrama de G(s)H(s) tiene n semicírculos de radio infinito, en sentido horario, en derredor del origen cuando el punto representativo s recorre el semicírculo de radio є (con є << 1). Por ejemplo, si la funciуn transferencia de lazo abierto siguiente.
G(S) H(s) = 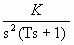
Entonces Criterio de estabilidad de Nyquist [Para un caso general en que G(s)H(s) tiene polos y/o ceros sobre el eje jω]: en el sistema que se ve en la Fig. 1, si la funciσn transferencia de lazo abierto G(s)H(s) tiene k polos en el semiplano derecho de s, para que haya estabilidad, a medida que el punto representativo recorre el diagrama de Nyquist modificado en sentido horario, el lugar G(s)H(s) debe incluir k veces el punto -1 + j0 en sentido antihorario.
En esta sección se presentan varios ejemplos ilustrativos del análisis de estabilidad de sistemas de control usando el criterio de estabilidad de Nyquist.
Si el recorrido de Nyquist en el plano s encierra Z ceros y P polos de 1 + G(s)H(s) y no pasa por ninguno de los polos o ceros de 1 + G(s)H(s) cuando el punto representativo s se desplaza en sentido horario a lo largo del recorrido de Nyquist, el contorno correspondiente en el plano G(s)H(s) encierra el punto - 1 + j0 N = Z - P veces, en sentido horario. (Valores negativos de N implican rodeos en sentido antihorario.) Al examinar la estabilidad de los sistemas de control lineales usando el criterio de estabilidad de Nyquist, se ve que se dan tres posibilidades.
1. No se encierra el punto - 1 + j0. Esto implica que el sistema es estable si no hay polos de G(s)H(s) en el semiplano derecho de s; en caso contrario, el sistema es inestable.
2. Hay uno o varios rodeos antihorarios del punto - 1 + j0. En este caso el sistema es estable si la cantidad de rodeos antihorarios es igual a la de polos de G(s)H(s) en el semiplano derecho de s; en caso de serio, el sistema es inestable.
3. Hay uno o varios rodeos del punto - 1 + j0 en sentido horario. En este caso, el sistema es inestable.
En los ejemplos siguientes se supone que los valores de la ganancia K y de las constantes de tiempo (como T, T, y T2) son todos positivos.
Ejemplo 1 - Sea un sistema de lazo cerrado cuya función transferencia de lazo abierto esta dada por:
G(s)H(s) = K/ (T1s + 1)(T2s+1)
Se pide determinar la estabilidad del sistema. En la Fig. 9 hay un diagrama de G(jω))H(jω). Como G(s)H(s) no tiene polos en el semiplano derecho de s y el punto - 1 + j0 no estα encerrado por el lugar, de G(jω)H(jω), el sistema es estable para cualquier valor positivo de K, T1, y T2.Ejemplo 2. - Sea el sistema con la función transferencia de lazo abierto siguiente:
G(s)H(s) = K / s(T1s + 1)(T2s + 1)
Se trata de hallar la estabilidad del sistema para dos casos:1. Ganancia K pequeña, 2. K elevada.
En la Fig. 10 se tienen los recorridos de Nyquist para función transferencia de lazo abierto con valor de K pequeño y elevado. La cantidad de polos de G(s)H(s) en la mitad derecha del plano s es cero. Por tanto, para que este sistema sea estable, es necesario que N Z = 0 o que el lugar de G(s)H(s) no rodee al punto - 1 + j0.
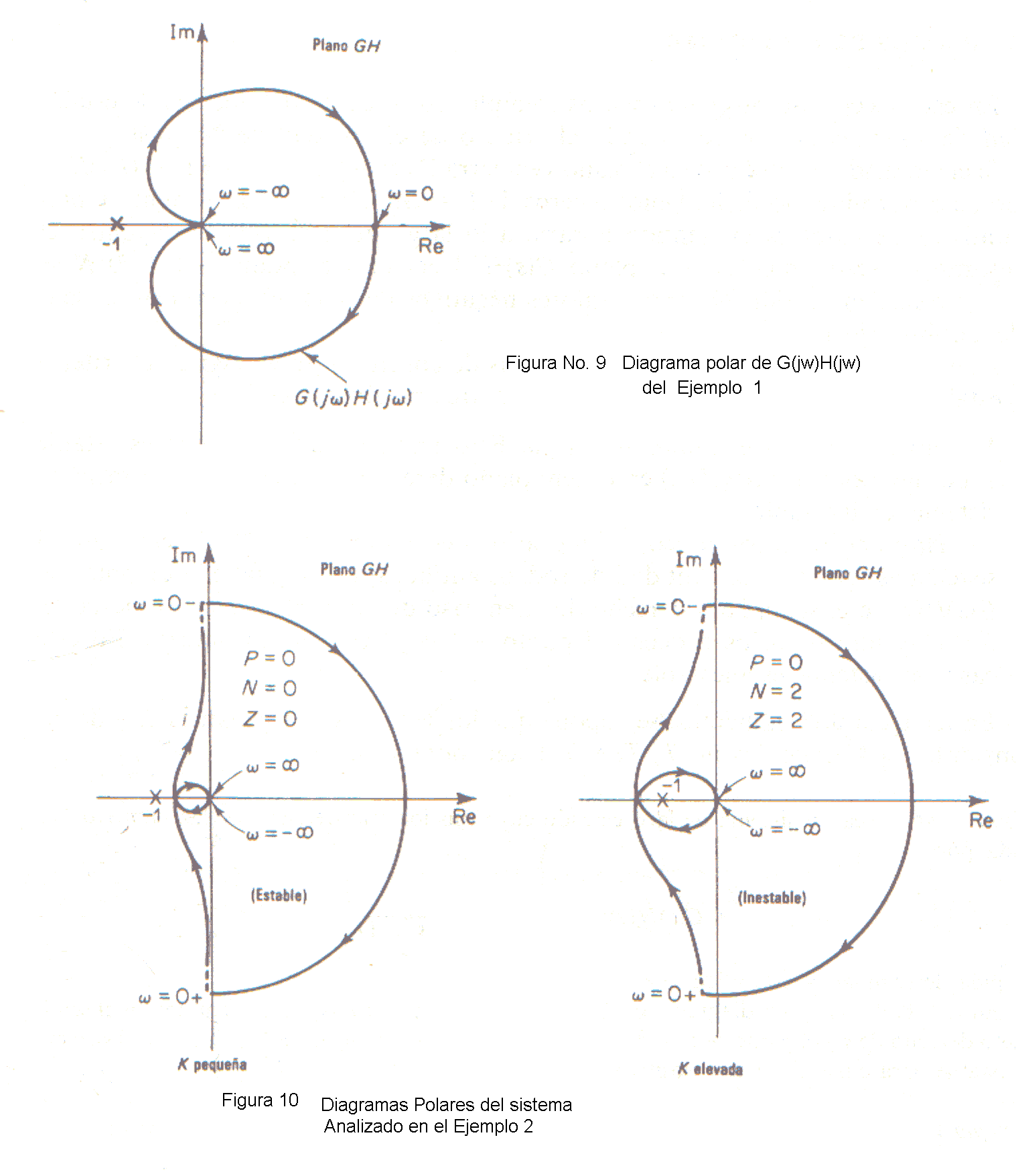
Ejemplo 3. – La estabilidad de un sistema de lazo cerrado con la función de lazo abierto siguiente:
G(s)H(s) = K(T2s + 1)/(s2(T1s + 1))
Depende de los valores relativos de T1 y T2 Se pide trazar los diagramas de Nyquist y determinar la estabilidad del sistema.En la figura 11 hay diagramas de los lugares de G(s)H(s) para los tres casos:
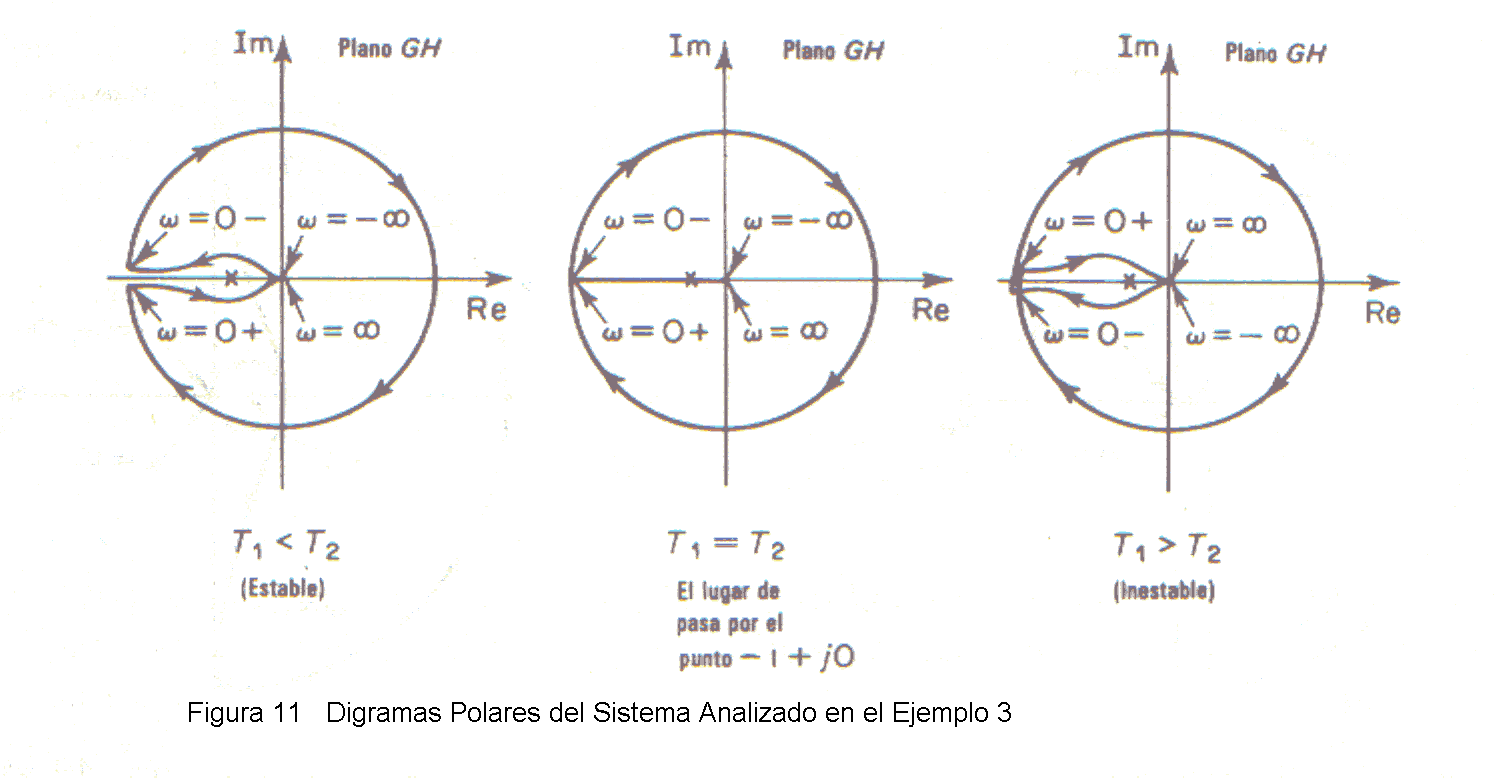
T1<T2 , T1=T2 y T1>T2 . Para T1<T2 , el lugar de G(s)H(s) no encierra al punto -1 +j0, y el sistema de lazo cerrado es estable. Para T1= T2 , el lugar de G(s)H(s) pasa por el punto -1 + j0 lo que indica que los polos de lazo cerrado están sobre el eje jω. Para T1> T2 , el lugar de G(s)H(s) rodea al punto -1 + j0 dos veces en sentido horario. Por ende, el sistema de lazo cerrado tiene dos polos de lazo cerrado en el semiplano derecho de s y el sistema es inestable.
Ejemplo 4. - Sea el sistema de lazo cerrado que tiene la funci6n transferencia de lazo abierto siguiente:
G(s)H(s) = K / s(Ts - 1)
Hallar la estabilidad del sistema.La función G(s)H(s) tiene un polo (s = 1/T) en el semiplano derecho de s. Por tanto, P =1.
El recorrido de Nyquist de la Fig. 12 indica que el mismo encierra el punto - 1 +.j0 una vez en sentido horario. Por tanto, N = 1. Como Z = N + P, resulta que Z = 2. Esto significa que el sistema de lazo cerrado tiene dos polos de lazo cerrado en el semiplano derecho de s y es inestable.
Ejemplo 5. - Estudiar la estabilidad de un sistema de lazo cerrado que tiene la función transferencia de lazo abierto siguiente:
G(s)H(s) = K(s+3) / s(s - 1)
La función transferencia de lazo abierto tiene un polo en (s =1) en la mitad derecha del piano s. El sistema de lazo abierto es inestable. El diagrama de Nyquist de la Fig. 13 muestra que el punto - 1 + j0 es rodeado una vez por el lugar de G(s)H(s) en sentido antihorario. Por tanto, N = - 1. Entonces, de Z = N + P, resulta que Z vale cero, lo que indica que no hay ningún cero de 1 + G(s)H(s) en el semiplano derecho de s, y el sistema de lazo cerrado es estable. Este es uno de los ejemplos en que-un sistema inestable de lazo abierto se vuelve estable al cerrar el lazo.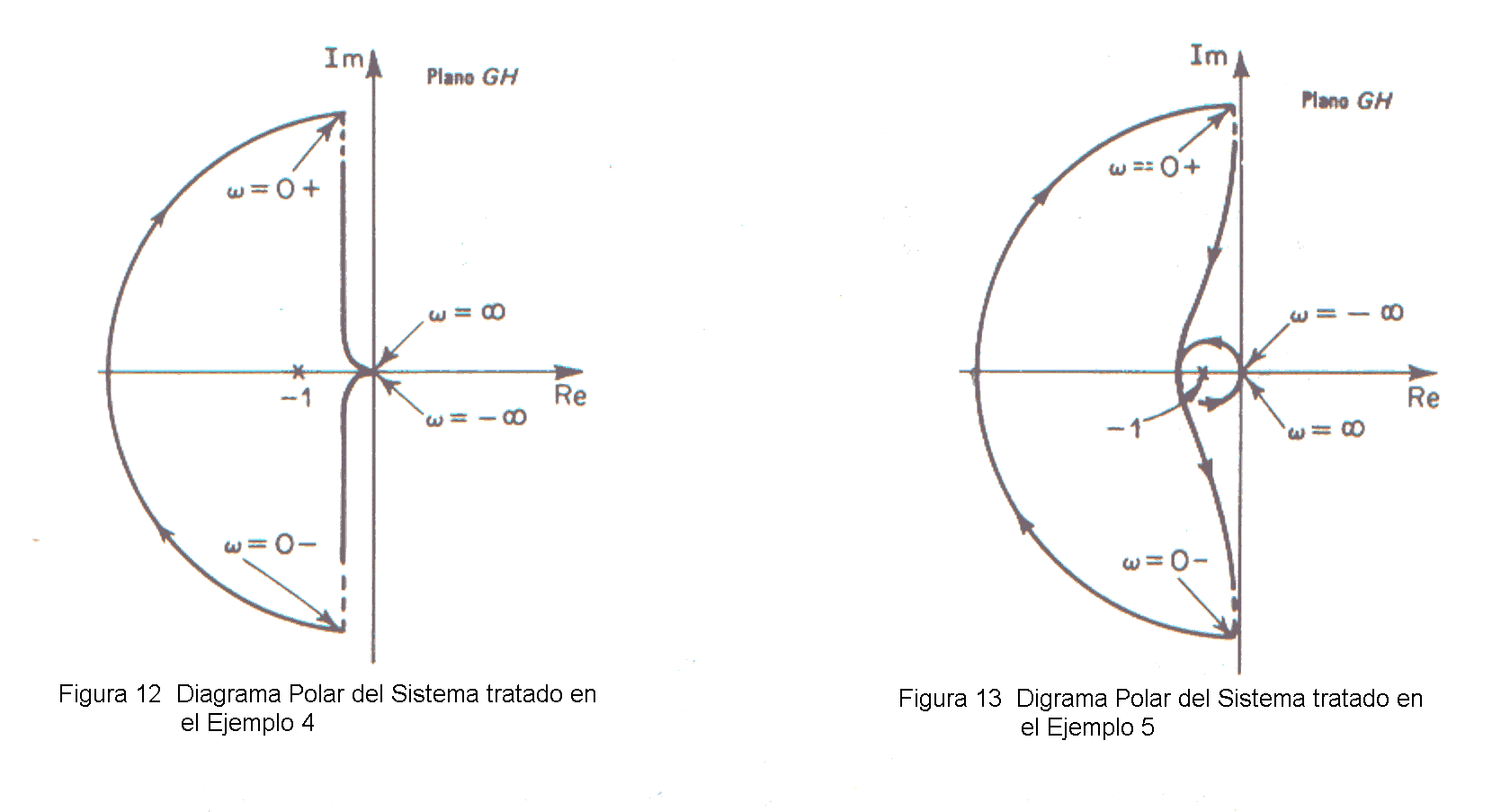
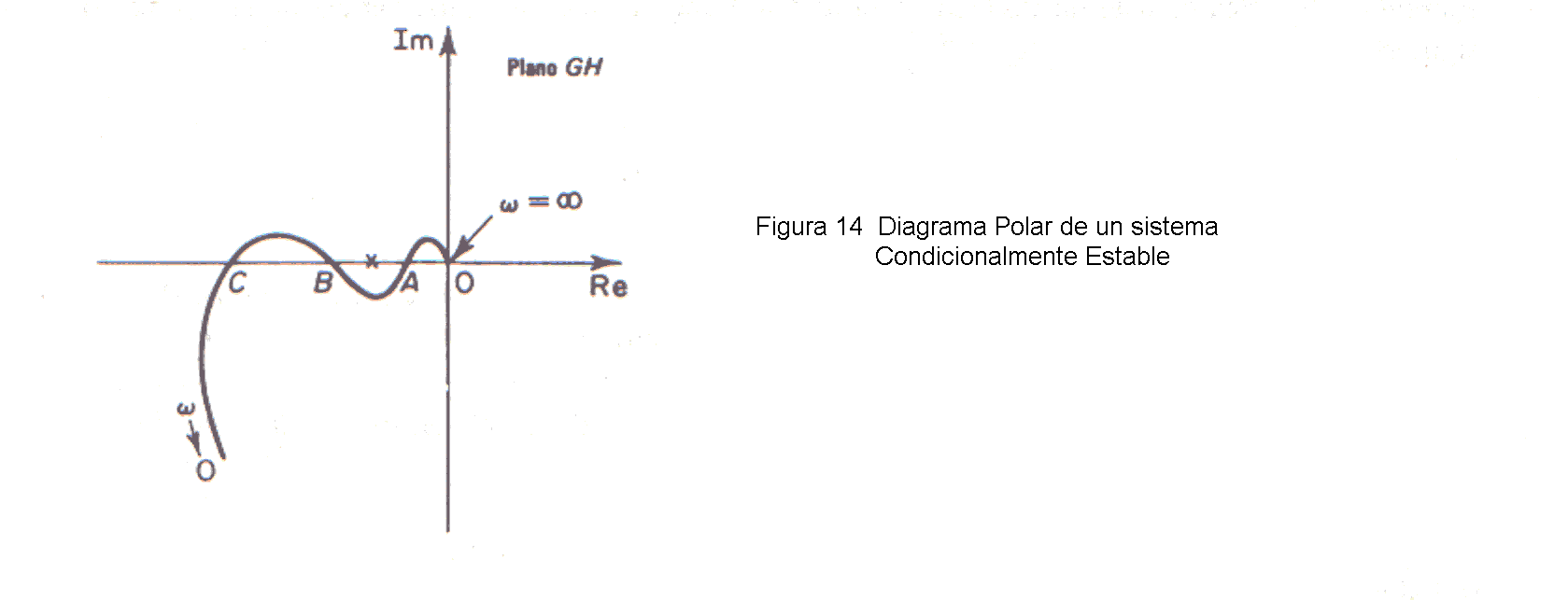
La figura 14 muestra un ejemplo en que el lugar de G(jω)H(jω) corresponde a un sistema de lazo cerrado que puede hacerse inestable variando la ganancia de lazo abierto. Si se aumenta suficientemente la ganancia del lazo abierto el lugar de G(jω)H(jω) encierra dos veces el punto - 1 + j0 y el sistema se hace inestable. Si en cambio, se disminuye suficientemente la ganancia de lazo abierto, nuevamente se da que el lugar de G(jω)H(jω) encierra dos veces al punto - 1 + j0. El sistema es estable solamente dentro de un rango limitado de valores de ganancia de lazo abierto, para los cuales el punto - 1 + j0 queda totalmente fuera del lugar de G(jω)H(jω). Un sistema asν es condicionalmente estable.
Un sistema condicionalmente estable es estable para valores de ganancia de lazo abierto comprendidos entre valores críticos, e inestable si la ganancia aumenta o disminuye suficientemente. Un sistema así se hace inestable al recibir señales de entrada grandes, ya que las mismas pueden producir saturación, la que a su vez reduce la ganancia del sistema a lazo abierto. Conviene evitar estas situaciones, pues el sistema se hace: inestable si la ganancia de lazo abierto cae por encima de determinado valor critico. Para un funcionamiento estable del sistema aquí considerado, el punto critico -1 + j0 no debe quedar en las zonas comprendidas por OA y BC, Fig. 14.
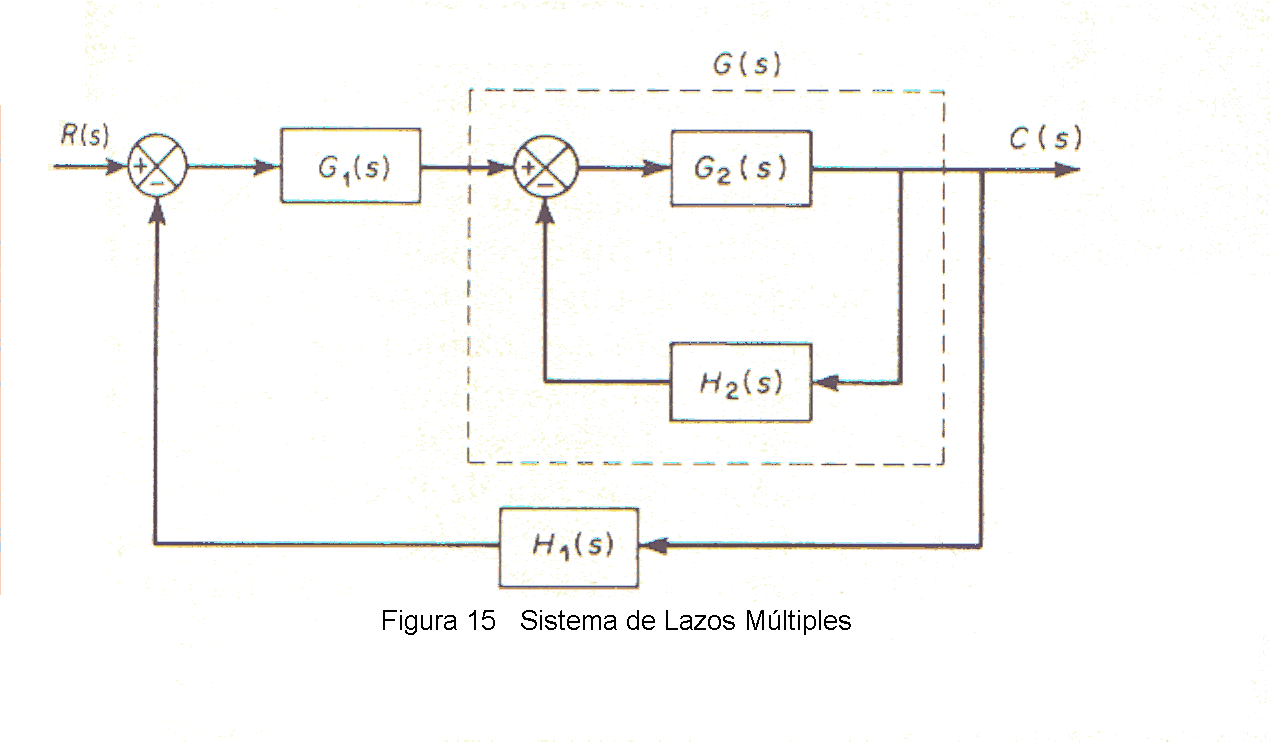
Sea el sistema que se ve en la Fig. 15. Se trata de un sistema de lazo múltiple. El lazo interior tiene la función transferencia
G(s) = G2(s) / (1 + G2(s)H2(s))
Si G(s) es inestable, los efectos de la inestabilidad consisten en producir un polo polos en la mitad derecha del plano s. Entonces la ecuación característica del lazo interno, 1 + G2(S)H2(S) = 0, tiene un cero o ceros en esta porción del plano. Si G2(s) y H2(s) tienen aquí P1 polos, se puede hallar la cantidad Z1, de ceros en el semiplano derecho de 1 + G2(s)H2(s), de Z1 = N1 + P1, donde N1, es la cantidad rodeos del punto - 1 + j0 en sentido horario, por el lugar de G2(S)H2(S) como la función transferencia de lazo abierto de todo el sistema esta dado por G1(s)G(s)H1(s), se puede hallar la estabilidad de este sistema de lazo cerrado con diagrama de Nyquist de G1(s)G(s)H1(s) y el conocimiento de los polos del semiplano derecho de G1(s)G(s)H1(s).
Publicado por: Karla Velasquez
No hay comentarios:
Publicar un comentario