La inestabilidad eléctrica tiene dos maneras de manifestarse, oscilando o quedándose de manera indefinida en alguno de los estados límite, que son out=+Vcc y out=-Vcc. Lo habitual es que las etapas oscilen, su salida alterna entre +Vcc y -Vcc a una frecuencia determinada.
Una etapa no debería quemarse, pero cuando oscilan lo hacen a frecuencias mayores de 1 MHz, donde las capacidades parásitas no son ninguna minucia y por ejemplo cargar los 2nF de los transistores de salida es un gran trabajo para la etapa, los drivers pueden estar enviando picos de corriente de 300mA y más. Ésto hace que a la larga se queme, pero no porque la inestabilidad sea peligrosa. Muchos circuitos no lineales como los temporizadores y los relojes se aprovechan de este fenómeno para funcionar.
Cuando un amplificador lineal es inestable no se puede utilizar, al igual que si se hace un avión que entra en sólo barrena tampoco conviene utilizarlo, pero se puede estabilizar.
Hay tres técnicas para compensar la respuesta y la más usada es la compensación por el efecto Miller. Las veremos a continuación.
Condiciones de inestabilidad
| La condición para ser inestable es que debe haber ganancia y que se realimente una señal desfasada más de 180º. Se debe pensar que la realimentación lo que hace es restar una parte de la salida a la entrada, un desfase de 180º supone que se está sumando en vez de restando, por eso se tiende a oscilar. | 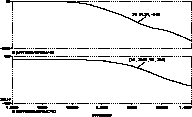 |
Un polo produce un efecto de filtrado paso-bajo, donde la respuesta cae 6dB/oct y se desfasa 90º en las frecuencias mayores de las que se encuentra el polo, con 45º y -3dB a la frecuencia del polo. Si conseguimos llegar al final de la banda (ganancia cero) con un desfase de menos de 180º, y menos de 135º preferiblemente, se estará evitando la oscilación, porque cuando se alcance el desfase de 180º ya no habrá ganancia y no se tiende a oscilar.
Un filtro paso bajo. ¿cómo se puede crear? Lo más normal es que se produzca por una capacidad parásita junto a una resistencia (RC). En la siguiente etapa de ejemplo tenemos una resistencia, Road1 y las capacidades parásitas base-emisor y base-colector del transistor QD. Tenemos también R4 y la capacidad parásita de QG, que en este caso se agrava por un fenómeno que comentaremos a continuación. En la gráfica vemos que la ganancia decrece a partir de una determinada frecuencia.
Esa es la realidad, las etapas no tienen un ancho de banda infinito, y se pueden crear multitud de polos. ¿qué pasa cuando se crean polos a frecuencias muy próximas? Que el desfase crece de manera muy rápida y la ganancia (habitualmente muy alta, >60dB) decrece muy lentamente, por lo que a alguna frecuencia el desfase de la salida será de 180º y tendremos ganancia suficiente como para que oscile.
| En ésta etapa de prueba (derecha), tal y como vemos en su gráfica de respuesta (diagrama de Bode de fase y de ganancia), el desfase de 180º tiene lugar a ~16 MHz. | 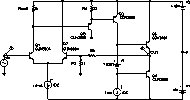 |
| A esa frecuencia la ganancia es de 51dB, por lo que oscilará cuando, en lazo cerrado, la ganancia mercada por la red de realimentación sea igual o menor que 51dB. Pero no oscilará cuando la ganancia sea superior a 52dB porque la ganancia "aparente" será menor que 1. |  |
¿Qué se puede hacer para evitarlo? Reducir la ganancia de manera que a la frecuencia crítica sea cero. Hay dos formas de hacerlo, una de ellas inadmisible desde el punto de vista de la ingeniería.
- Prescindir de la realimentación o reducir de manera drástica la cantidad.
- Compensar en frecuencia.
Es obvio cual de las dos técnicas se aplica. Hay tres maneras de compensar en frecuencia:
- Polo dominante
- Polo-cero
- Compensación por el efecto Miller.
Sólo nos ocuparemos de la técnica de compensación por el efecto Miller, las otras son inviables o desaconsejables.
UN POCO DE TEORÍA.
Antes de seguir debemos introducir dos conceptos que marcan cómo de estable es una etapa: el margen de fase y el margen de ganancia.
| El el gráfico de la derecha podemos ver cómo se miden estas cifras. Existen dos frecuencias relevantes, f0 y f180 , marcan los puntos en los que la ganancia se hace igual a uno (0 db, f0) y la frecuencia en la que la fase es igual a 180º, f180. |  |
Se entiende como margen de fase la diferencia de fase entre f
0 y f
180, así como el margen de ganancia es la diferencia en la ganacia entre f
180 y f
0. Como es lógico, cuanto mayores sean estas cifras, mayor será la estabilidad de la etapa.
En la práctica conviene trabajar con márgenes holgados, si no se corre el riesgo de que las condiciones externas modifiquen éstos márgenes, como por ejemplo cargar con un condensador (cable), que reduce el margen de fase. El mínimo margen de fase recomendable es de 45º y el mínimo de ganancia, 10dB, pero cuanto más, mejor.
COMPENSACIÓN POR EL EFECTO MILLER.
| El efecto Miller consigue estabilizar las etapas creando un polo a baja frecuencia que es el responsable de disminuir la ganancia para que a las frecuencias en las que se produce el desfase de 180º la ganancia sea menor que 1 (0dB). | 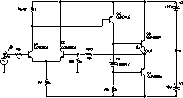 |
En esta etapa de prueba tenemos que la ganancia cuando la fase es de 180º, a 35 MHZ, es de +16dB, por lo que no será estable para ganancias menores.
Sin embargo, aún se puede hacer algo más. | 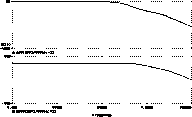 |
| Vemos en la gráfica como añadiendo un condensador entre la base y el colector de QG se obtiene la gráfica mostrada abajo, en la que la etapa ya es estable, y con un margen de fase y de ganancia más que suficientes. | 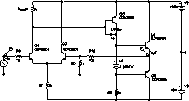 |
| La función de este nuevo condensador es crear el polo a baja frecuencia que hará que la etapa sea estable, y de hecho el polo está a 480 Hz (-3dB) , lo que en la gráfica anterior no aparecía. |  |
Ahora pasamos al efecto Miller en sí mismo: ésta técnica consiste en aprovechar un fenómeno parásito para producir el polo, que es un filtrado RC.
Si tenemos en cuenta que las resistencias internas de los op-amp y etapas suelen estar en torno a 2k y que se suelen poner polos a frecuencias tan bajas como 10 Hz, 1 Hz, 0,1 Hz... los cálculos mandan que el condensador debe ser de 10, 100 ó 1000 uF. Dentro de un op-amp es imposible hacer un condensador tan grande, y saldría carísimo porque el área de siilcio es muy cara.
En el esquema de la derecha vemos qué es lo que sucede. Dada una etapa de amplificación, el condensador existente entre la entrada y la salida se divide en dos condensadores equivalentes (derecha) con los siguientes valores:
C!=CMiller*(Av+1)
C2=CMiller*((Av+1)/Av)) | 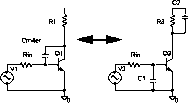 |
Vemos pues que el condensador C1 puede alcanzar valores muy grandes dependiendo del valor del condensador inicia y del valor de la ganancia de la etapa. El condensador a la salida es de un avalor mucho más bajo, más dependiente del valor de C
Miller original y no de la ganancia.
De esta manera, C1 y Rin forman un filtrado de paso-bajo que se comporta como un polo dentro del conjunto de una etapa. Siguiendo con el ejemplo anterior, si la etapa tiene ganancia 100.000 (100dB), el condensador necesario ya no sería de 10 uF sino 100.000 veces menor, 100pF, que si que se puede hacer en el interior del op-amp.
Pero hay más, éste condensador es responsable del ancho de banda de la etapa, eso es obvio, pero también de su slew-rate. Compensar para ganancia unidad es lo que mayores condensadores requiere, pero si compensamos para ganancia 10, podemos extender el ancho de banda 10 veces y también el slew-rate (más o menos). Y si la red de realimentación de la etapa está preparada para ganancia 10 no habrá inestabilidad porque elevamos la condición de ganancia.
SLEW-RATE
El
slew-rate es una medida de cómo de rápido pueden variar los voltios de la salida frente al tiempo. Habitualmente se mide el voltios dividido por microsegundo. (V/us)
El condensador de Miller del que hemos hablado antes es un condensador que se tiene que llenar y vaciar de carga alternativamente, y ésto lo hace a través de las mallas que lo controlan.
En el caso de una etapa normal como la mostrada a la derecha, la malla es la rama inversora de la etapa diferencia, y ésta rama tiene limitada la corriente, porque se alimenta a través de una fuente de corriente. | 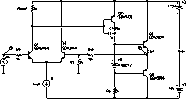 |
Para determinadas condiciones, las más comunes en las topologías habituales, el slew-rate está determinador por la corriente de la fuente I3 ,I(I3), dividido por la capacidad parásita (o no) C
Miller, por lo que SR=I/C
Miller.
| El el caso de que I3 no fuese una fuente de corriente sino una resistencia se pueden hacer cálculos aproximados mediante la ley de Ohm. El voltaje en esta resistencia prácticamente es fijo, por lo que en el caso de la derecha podemos estimar que R7 equivale a una fuente de corriente de 1.43mA |  |
Un caso especial son las etapas de realimentación en corriente. En ellas no hay ninguna fuente de corriente que limite la carga del condensador de compensación, por lo que la carga se aproxima a una carga RC, que tiene forma exponencial en vez de la carga en forma de rampa habitual en la carga de un condensador mediante una fuente de corriente.
La carga exponencial ofrece pendientes de variación muy altas al principio y que éstas por sí mismas tienen pendiente infinita al inicio. | 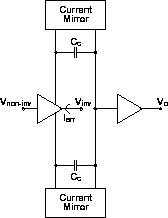 |
En un caso más real si que existen limitaciones en el
slew-rate en las etapas de realimentación en corriente, pero éstas limitaciones son mucho menores, permitiendo obtener con facilidad tasas de
slew-rate 10 veces mayores que el las etapas de realimentación en voltaje. Éstas limitaciones se deben principalmente a un fenómeno muy común.
Existen resistencias en el lazo de realimentación y en el camino de la señal a través de las cuales se cargan los condensadores de compensación. Dentro de un operacional, por muy grande que sea la sobrecarga no se puede superar el voltaje de alimentación, y llega un punto que las etapas se saturan y las resistencias no admiten más voltaje. Éste caso ya lo hemos visto antes, se trata de una resistencia con un voltaje fijo, que equivale a una fuente de corriente y de ésta manera se limita el
slew-rate en este tipo de etapas.
¿Por qué es tan importante el
slew-rate? Es una cifra muy infravalorada, cuando gran parte de las características sonoras de una etapa dependen de ella.
| Lo primero, porque crea distorsión y compresión.sonora. Vemos en la gráfica de la derecha cómo la limitación de slew-rate crea una distorsión semejante a un diente de sierra en una onda senoidal. Esta distorsión es medible y es una de las causas junto a las capacidades no lineales de que la distorsión armónica crezca con la frecuencia. Recordamos también que IMD y THD van juntas, y que IMD se agrava cuando la función de transferencia se hace menos lineal. | 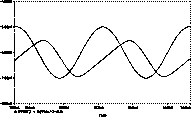 |
Lo mostrado en la gráfica anterior se comoce como TIM (
transient intermodulation) o SID (
slew induced distortion), decubiertas por Mati Ottala, científico escandinavo de gran prestigio y autor de etapas míticas como el EC 25W de Electrocompaniet.
Lo segundo, porque es causa de sobrecargas en las etapas. Ésto se conoce como hard TIM y es causa de características sonoras que no se pueden medir con THD. Es muy próxima a una distorsión de memoria, tiene como efectos la saturación de los nodos internos de la etapa y la entrada en corte o saturación profunda de muchos de sus transistores. Esto tiene retrasos temporales serios y que son causa de baja coherencia en el sonido de una etapa. Más aún, si éstos retrasos y salidas del punto de operación tienen una recuperación lenta producen sonidos claramente audibles y que se suelen denominar "grano". Éste fenómeno se ve agravado por las altas cifras de ganancia en lazo abierto, es la causa de que la válvulas con slew-rate's muy pobres no tengan "grando".
Está probado por la psicoacústica que las primeras partes de un sonido impactante son las que marcan nuestra respuesta emocional a ese sonido impulsivo. Una limitación en la amplitud de la señal al inicio es motivo de que nuestro oído perciba compresión sonora, y en las etapas ésto tiene una causa evidente en TIM y hard TIM.
Y esta es la respuesta a la pregunta ¿porqué se hace tan alto el ancho de banda de las etapas si no oímos más allá de 20 kHz?
OP-AMP de aplicaciones especiales y casos reales.
Hemos visto en el apartado de "compensación por efecto Miller" que para hacer estable un amplificador se requiere reducir el ancho de banda y ésto también reduce su
slew-rate. Sin embargo, sabemos que para grandes ganancias no es necesario utilizar compensaciones tan estrictas, podemos relajar la condición de margen de ganancia y hacer etapas con un mayor ancho de banda y
slew-rate. En el mercado existe op-amp subcompensados que dan mayores cifras de ancho de banda y slew-rate, son necesarios para aplicaciones con gran ganancia como DACs, previos RIAA, previos de micro y me refiero a los uA748, NE5534, OP37, OPA637,...
Es curioso que su coste sea mayor, cuando los costes de fabricación son menores por el menor tamaño del condensador, aunque también influye en su coste el menor volumen de ventas.
| Como ejemplo, podemos ver los OPA27 y OPA37 de Burr-Brown, unos operacionales de bajo ruido y precisión. El OPA27 es un op-amp compensado para ganancia unidad y el OPA37 es el mismo OPA27 pero compensado para ganancias mayores que 5. | 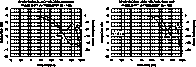 |
En ella podemos comparar el ancho de banda y fase para un lazo cerrado de ganancia 100, 40dB. En el OPA27 el ancho de banda es de 30 kHz mientras que el OPA37 es de 300 KHz, lo que evidentemente para ésta ganancia es mejor y también para ganancias mayores que 5 también. Con la salvedad de que no puede usarse en todos los casos.
El NE5534 es un operacional subcompensado, estable para ganancias mayores que 3, y muy usado por su bajo coste. Al igual que muchos otros operacionales permite la adición de un condensador externo que sirva para compensar en frecuencia.
Mediante el cambio de éste condensador podemos ver cómo el slew-rate pasa de 13 a 6 V/us por la adición del condensador externo de compensación, y cómo a alta frecuencia la limitación de slew-rate impide proporcionar señales de la misma amplitud que a baja. | 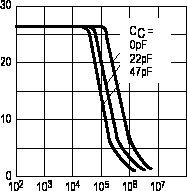 |
Tenemos por otro lado los op-amp de realimentación en corriente, otro mundo aparte de las restricciones habituales de los operacionales de realimentación en voltaje. En ellos la estabilidad se marca también un grupo RC, pero ésta resistencia no es fija y la estabilidad no depende de la ganancia del lazo cerrado sino de esta resistencia, externa y presente en el lazo de realimentación.
| Vemos en la gráfica de respuesta en frecuencia normalizada de un OPA684 de Burr-Brown, de realimentación en corriente. Prácticamente no hay cambios en el ancho de banda, y lo único que cambia es la "Q" al final de la banda. Se trata de un operacional con un ancho de banda superior a 120 MHz y un slew-rate de aproximadamente 700V/us | 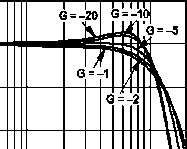 |










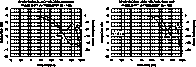


No hay comentarios:
Publicar un comentario