Uses:
In addition to determining the stability of the system, the root locus can be used to design for the damping ratio and natural frequency of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant natural frequency can be drawn as arcs whose center points coincide with the origin. By selecting a point along the root locus that coincides with a desired damping ratio and natural frequency a gain, K, can be calculated and implemented in the controller. More elaborate techniques of controller design using the root locus are available in most control textbooks: for instance, lag, lead, PI, PD and PID controllers can be designed approximately with this technique.
The definition of the damping ratio and natural frequency presumes that the overall feedback system is well approximated by a second order system, that is, the system has a dominant pair of poles. This often doesn't happen and so it's good practice to simulate the final design to check if the project goals are satisfied.
From the function T(s), we can also see that the zeros of the open loop system (CP) are also the zeros of the closed loop system. It is important to note that the root locus only gives the location of closed loop poles as the gain K is varied, given the open loop transfer function. The zeros of a system can not be moved.
Using a few basic rules, the root locus method can plot the overall shape of the path (locus) traversed by the roots as the value of K varies. The plot of the root locus then gives an idea of the stability and dynamics of this feedback system for different values of k.
The method is due to Walter R. Evans
Sketching root locus
- Mark open-loop poles and zeros
- Mark real axis portion to the left of an odd number of poles and zeros
- Find asymptotes
| ∑ |
| P |
| ∑ |
| Z |
and P is the number of poles and Z is the number of zeros
- Phase condition on test point to find angle of deparature
- Compute breakaway/break-in points
The break-away (break-in) points are obtained by solving a polynomial equation
z-plane versus s-plane
The root locus can also be computed in the z-plane, the discrete counterpart of the s-plane. An equation (z = esT) maps continuous s-plane poles (not zeros) into the z-domain, where T is the sampling period. The stable, left half s-plane maps into the interior of the unit circle of the z-plane, with the s-plane origin equating to z = 1 (because e0 = 1). A diagonal line of constant damping in the s-plane maps around a spiral from (1,0) in the z plane as it curves in toward the origin. Note also that the Nyquist aliasing criteria is expressed graphically in the z-plane by the x-axis, where (wnT = π). The line of constant damping just described spirals in indefinitely but in sampled data systems, frequency content is aliased down to lower frequencies by integral multiples of the Nyquist frequency. That is, the sampled response appears as a lower frequency and better damped as well since the root in the z-plane maps equally well to the first loop of a different, better damped spiral curve of constant damping. Many other interesting and relevant mapping properties can be described, not least that z-plane controllers, having the property that they may be directly implemented from the z-plane transfer function (zero/pole ratio of polynomialls), can be imagined graphically on a z-plane plot of the open loop transfer function, and immediately analyzed utilizing root locus.Since root locus is a graphical angle technique, root locus rules work the same in the z and s planes.
The idea of a root locus can be applied to many systems where a single parameter K is varied. For example, it is useful to sweep any system parameter for which the exact value is uncertain, in order to determine its behavior.
.Publicado por: Karla Velasquez


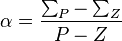

No hay comentarios:
Publicar un comentario